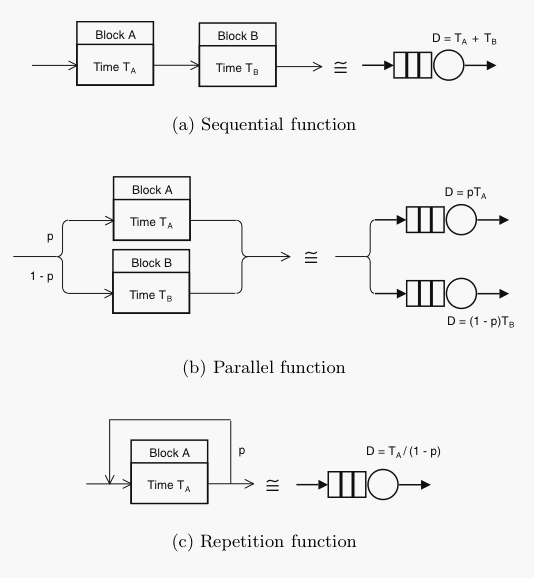
Since all digital computers and network systems can be considered as a collection of functional blocks and these blocks often contain buffers, their performance can be modeled as a collection of buffers or queues. Therefore, start developing your PDQ model by drawing a functional block diagram of the relevant architecture using elements like these:
The objective is to identify how much time is spent at each stage or block as it processes the workload of interest. Ultimately, each functional block becomes converted into a queue subsystem like those shown above. This includes the ability to distinguish sequential and parallel processing. In the language of PDQ, a queue is created using a call to either CreateNode or CreateMultiNode.
Here's how the above blocks would appear in PDQ in R as three separate models in the same R script:
# PDQ fun blocks
# Created by NJG on Mon Aug 30 2010
library(pdq)
work <- "Requests"
arate <- 0.75
Ta <- 0.25
Tb <- 0.75
p <- 0.5
Init("Sequence Fun Blocks")
CreateOpen(work,arate)
CreateNode("SeqBlock",CEN,FCFS)
SetDemand("SeqBlock",work,Ta+Tb)
Solve(CANON)
Report()
Init("Parallel Fun Blocks")
CreateOpen(work,arate)
CreateNode("ParaBlock1", CEN,FCFS)
SetDemand("ParaBlock1",work,p*Ta)
CreateNode("ParaBlock2",CEN,FCFS)
SetDemand("ParaBlock2",work,(1-p)*Tb)
Solve(CANON)
Report()
Init("Repetition Fun Blocks")
CreateOpen(work,arate)
CreateNode("RepBlock",CEN,FCFS)
SetDemand("RepBlock",work,Ta/(1-p))
Solve(CANON)
Report()
We can easily check the output of the "Sequence Fun Blocks" model. Since the combined service demand equals 1.0 second and the arrival rate is 0.75 per second, the residence time (R) had better be R = 1/(1 - (3/4)) = 4 seconds. And indeed, the RESOURCE Performance section of the PDQ Report reveals that to be correct.
****** RESOURCE Performance *******
Metric Resource Work Value Unit
------ -------- ---- ----- ----
Throughput SeqBlock Requests 0.7500 Trans/Sec
Utilization SeqBlock Requests 75.0000 Percent
Queue length SeqBlock Requests 3.0000 Trans
Waiting line SeqBlock Requests 2.2500 Trans
Waiting time SeqBlock Requests 3.0000 Sec
Residence time SeqBlock Requests 4.0000 Sec
Other diagrammatic techniques e.g., UML diagrams, may also be useful but I don't understand that stuff so I've never tried it. If anyone does try that approach I'd be interested to hear about it.
See Chap. 6 "Pretty Damn Quick(PDQ)—A Slow Introduction" in my Perl::PDQ book for more ideas.
11 comments:
dear Dr. Gunther,
I'm currently reading your book "analyzing computer system performances with perl:PDQ"
after having discovered your wonderful blog.
Since I would like to model an online charging process I'm struggling to find an example
that looks like it with no luck.I would like to have some hints from you to choose the best model.
In an online charging an user (an online game player, a person making a mobile phonecall)
has a certain amount of credit that is consumed while it uses the service (it is a prepaid service).
When he starts a new call (or a game session) a specific amount of money is reserved and deducted from his credit
and a specific service time portion is granted to use the service. When time is over, another authorization request
is made, until user closes his session or credit is over.
Let's suppose that I have 40 new session starting per second, and interim authorizations happen every 30 seconds.
Also, the system takes 0.2 seconds (service time) to answer each authorization request (initial, interim and termination).
Last, I would set average session duration to 120 sec for mobile calls or 1800 sec for online game sessions.
I would say that, in case of mobile calls, I have 5 authorizations (init, 30, 60, 90, term), hence
my arrival rate is 150 req/s.
Here is my first doubt: init authorizations are markovian, but following depend from init;
can I consider them markovian as well and so summable?
The presence of these feedbacks confuses me because if there were only init authorizations
I would use an open queue model, but since the subsequent requests depend
on the first, it resembles a closed queue, with finite
number of users (active session users).
Time between requests is 30 sec; should I use a delay node to simulate it?
I'm considering it as think time, am I correct?
Could you please put me back on track?
Thanks in advance
Fresio
Hi Fresio,
A very nice example and a good question, which is certainly soluble.
Since it's a bit involved, however, I'll address it in an upcoming blog post.
--njg
On further reflection, although I know what you are asking me from the modeling standpoint, there is one thing missing: What question are you trying to answer with your PDQ model?
Put another way: What outcome are you looking for?
The reason it is always worthwhile to ask yourself this question is that it can help you to organize your PDQ model inputs (the stuff you write in the PDQ code) from PDQ outputs (the stuff you find in the PDQ Report).
For example, if you wanted to determine the throughput of the gaming system, then you couldn't define your PDQ model to be an open queueing model because throughput (or equivalently, the arrival rate in steady state) is a required input parameter for an open PDQ model.
As your description stands right now, you kinda have a pile of somewhat undifferentiated numbers. Nothing wrong with that, and we all start with something like that. Just sayin' that sorting your inputs from your outputs would be a good next step.
Hi,
my main goal is to understand how many parallel queueing centers (cpus) would I need to get a reasonable response time, let's say under 0.5 seconds, given an arrival rate of 40 new sessions/second and a session update (new interim authorizations) every 30 seconds.
I can hypothesize a service time because I can measure an alpha version of authorization routine that takes 0.2 seconds to complete.
After that, I would like to make a boundary analysis (as described in your book) to understand what will be the limits of this system. When I got a good model to represent my architecture, as you would imagine, I'll start my imagination and simulate the system behaviour by changing service time, number of cpus, delay between interim request to understand which is the part that gives the highest performance and scalability improvements. Response time must stay under 0.5 second 90% of the time, to make it realistic.
Thanks
While we're about it, let's do some bounds checking before we build any PDQ models.
It appears that you will have at least 2 resources: authent and session. In the mobile-calls model, I can glean their respective service times as:
1. S_authent = 0.20 s
2. S_session = 30.0 s
The largest of these (Smax) is (2), the session time.
Using eqn.(5.3) on p. 193 of the PPDQ book gives us the bound on allowed throughput (Xmax) or, what is the same thing for an open queueing circuit, the max arrival rate of requests (e.g., calls). Since 1/Smax = 0.0333 calls/s, I don't see how "40 new sessions/second" can be accommodated.
Put differently, the PDQ model won't solve with these input parameters.
I realize you may be thinking that S_session = 120 s in the mobile model, but that is the total service demand, which can be achieved by visiting the session resource 4 times, in between the authent servicing. In other words, the session servicing is time-sliced as part of the feedback between it and the authent service; the modeling step that is bothering you.
Overall, any choice of service times other than the one I've used above is likely to be longer and therefore, the bound on allowed arrivals will be even lower than the example I've given.
What am I missing?
30 seconds is the distance between 2 successive authorization requests from the same session. I don't see it as a service time. In that timeslice there is no computation for the same mobile call. In other words, if there where only 1 call active, in the time between 2 successive authorization requests the system (that accounts only for credit management) would be completely idle. Sorry for not being clear. I hope this clarifies. Of course, there will be other systems in the platform that will be busy for all the session time, eg. the gaming server that broadcast data about other players, or the mobile network devices that serve the call. Thanks
Then explicitly identify the respective service times as you see them and show me how they reconcile with your claim of 40 new sessions/second.
I'll give it a try. I'm focusing only on credit management server. In a time window of 10 minutes it will receive 600X40X5 = 120000 calls, hence 200 calls per seconds on average (I'm multiplying by n. of call by 5 visits). each call is answered in 0.2 sec (service time), giving a resource need of 40 seconds per second; this means that I would need 40 cpus working at 100% load. Of course this will make wait time be huge, so I need to understand how many cpu would I need to have a Response time of 0.5 seconds (or how much should I improve my service time to reduce n of cpu to a reasonable quantity). I'm getting the same results using bounds checking eqn (5.3); service demand D = VxS -> 5x0.2 = 1 second, Xmax = 1/Dmax = 1/1. This (I believe) tells me that only 1 call per second can be completely served by each cpu, so I need 40 cpu to serve 40 calls per seconds. I'm hesitant, does this make sense? 40 new session per second is an input parameter, it is the expected load at peak time.
Well, I'm certainly glad you are trying and I don't want to discourage you, but you begin to see why I don't normally carry on this kind of discussion as a blog commentary. I can't read your mind and you don't have my expertise, so it quickly becomes an endless dance trying to understand each other.
We seem to be quite a distance away from your initial description, as I read it. What happened to the 30 s interim delays for credit deduction?
What happened to the "feedback" you alluded to in your initial description?
What you are now describing seems to be nothing more than an M/M/m queue or CreateMultiNode() in PDQ, where you'd like to determine the size of m.
In that case, you've almost answered your own question.
If indeed your service demand is just D = 5 * 0.20 s, as you now assert, then that's the best you can do (on average), no matter how many "cpus" you have.
Moreover, you cannot attain a mean response time of better than R = 1 s because Rmin in your current description is just D.
So now, I'm confused (again) as to what question you are really trying to address with your PDQ model. If it's to achieve an R <= 0.5 s, then the only thing you can do is reduce the service demand, e.g., with fewer visits.
I would like to thank you for your patience. Maybe I'd better send you a document describing what I have in mind instead of trying to explain with a few words in a blog comment, if I can get an email address. Response time I cited is intended for the single authorization request; if S=0.2s then R<= 0.5s is my target; if I consider total service demand D=1, then R <= 2.5s is my target. Since for every mobile call I get 5 authorization requests, each with 30 seconds of delay from the preceding, I imagined a model that receives the first authorization request from an external source (users), and for each of them I get 4 further requests. I imagined these 4 further requests as a feedback generated from the first one, but with the 30 seconds delay. It seems that I was wrong and I can get what I need using a mere open queue with no feedback and a service demand = 0.2s x 5 visits. In this way the only outstanding question is how many cpu do I need to serve my load. I just tried o apply eqn. 2.44 in your book to get Response Time in parallel queues and with trial end error I found that I need 67 cpu to match my response time constraint. If I set n of visits v=4, D=0.8, R=2 I need 53 cpu. Reducing service time of just 10%, with v=4, D=0.72, R=2 I need 45 cpu. Thats fun! I'm currently using excel, I'll try to use pdq. I'm in the right path now?
Thanks
No harm done. Come and read PDQ Models: Show Me the Code.
In fact, this discussion has led me to think of some new ideas for PDQ, but more on that later.
Post a Comment